
The solution to this Latin anagram published by Robert Hooke (1635-1703) is the following “Ut pendet continuum flexile, sic stabit contiguum rigidum inversum”, the translation is “As hang the flexible line, so but inverted will stand the rigid arch”.
The concept is simple: in order to obtain an arch that acts in pure compression, the shape of the equivalent hanging chain needs to be inverted. This is one of the first steps done to formalize the idea of funicularity. Funicular structures adopt the right shape in accordance with the applied load and funicular shells are ideally able to resist external loads using axial force only, without introducing bending. As a result their thickness can be minimized and the amount of material reduced. Since the construction industry is largely responsible for CO2 emissions, efficiency and reduced use of material should be the target for every designer.
However an ideal funicular behavior is subject to specific conditions: the boundary conditions are congruent with the selected structural shape and the applied load, and the ratio between membrane stiffness and the flexural stiffness tends to infinity. When designing real shells these conditions are not always satisfied and bending moments, even if minimal, arise. Even if this happens, limiting the flexural component is fundamental and so we can introduce a relaxed definition of the term funicularity. If bending moments exist but give a contribution much smaller than that of the membrane forces, the shell is not funicular but can be defined R-Funicular!
The definition of R-Funicular shells depends on the application of the Relaxed Funicularity Ellipse Method formulated to quantify the funicularity and provide insights into the structural efficiency of the selected shape. The method uses a generalized definition of the eccentricity that is calculated in every point of the given surface as the ratio between the bending moment and the axial force acting along a given direction. The structure is considered R-Funicular if the calculated eccentricity is included into an admissibility interval that depends on the shell thickness and on a parameter set by the designer. Hence the condition of R-Funicularity is verified if the bending moments give a contribution much smaller compared to the one provided by the membrane forces in the structural capability of the shell. The method is suitable for an interesting graphical representation.

We can draw an ellipse, as the black one represented in figure, for every node of the shell analyzed. Every point of the ellipse is associated to a couple of moment M and axial force N acting in a given direction. The slope of the blue lines tangent to the ellipse represents maximum and minimum eccentricities, while the one of the red lines represents the limiting values of the eccentricities. If the ellipse is contained in the area delimited by the red lines the shell is R-Funicular in the node considered and viceversa.
The R-Funicular Ellipse Method has been applied to a number of form found shapes to validate it. Some results are shown below. For the form found catenary vault shown in figure, the method has been applied to some nodes characteristic of the different behaviors across the surface.
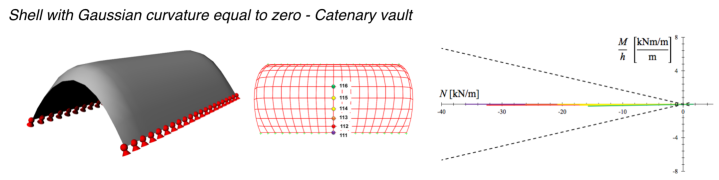
As one can observe, all ellipses degenerate into line segments flattened on the N axis confirming that the shell has a bending-free behavior and is R-Funicular.


For the shell with positive Gaussian curvature, looking at the output obtained applying the R-Funicular Ellipse Method, we can easily guess which is the best option, in term of thickness, under two different loading conditions: self-weight (used in the form-finding process) and self-weight plus horizontal loading.
In order to apply the method in a faster and efficient way, a beta version of the R FUN software is being implemented in Matlab®. After analyzing the selected shell using the FE package SAP2000, the R-FUN tool is able to import the results obtained in terms of internal forces. Applying the R-Funicular Ellipse Method, the eccentricities in every node are calculated, the ellipses are visualized and the areas of the shell where the R-Funicular condition is verified or not are given.
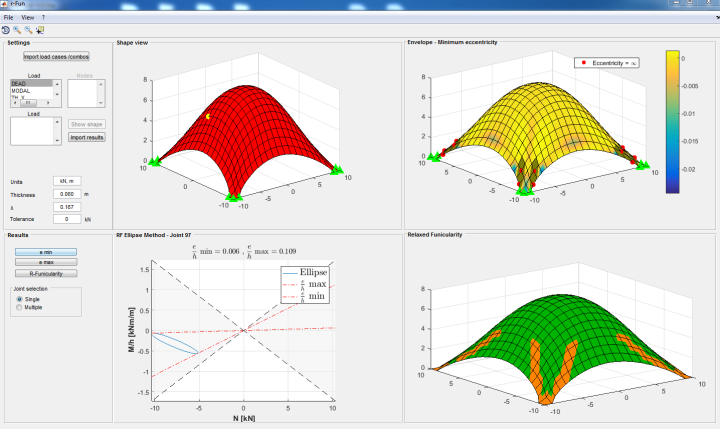
Author Giulia Tomasello, PhD student Roma Tre University and Visiting Student Research Collaborator at the Form Finding Lab, Princeton University
References
S. Gabriele, V. Varano, G. Tomasello, D. Alfonsi, “R-Funicularity of form found shell structures,” Engineering Structures, vol. 157, pp. 157-169, 2018.
Acknowledgments
The R-FUN software is being developed by G. Acunzo (post-doc at Dep. of Mathematics and Physics, University Roma Tre) and G. Tomasello (PhD Student at Dep. of Engineering, University Roma Tre, Visiting Student Research Collaborator at the Form Finding Lab at the Department of Civil and Environmental Engineering, Princeton University), and works under the supervision of S. Gabriele and V. Varano (Dep. of Architecture, University Roma Tre).

